Умение преобразовывать шестнадцатеричные числа может быть полезно не только программистам, но и дизайнерам, ведь триада RRGGBB есть не что иное, как «машинные» компоненты для красного, зелёного и синего соответственно — от 0 до 255 каждое. Конечно, графические редакторы содержат палитры со встроенными преобразователями, а стандартный калькулятор операционной системы умеет справляться с этой задачей, но порой гораздо удобнее самому «накинуть +14» к требуемой компоненте, а не запускать сторонние программы.
Прежде, чем я покажу, как (легко) можно переводить числа из шестнадцатеричной системы и более привычную для нас, необходимы дополнительные мероприятия. Все мы в школе учили таблицу умножения, и можем убедиться, что данный навык остался (хотя некоторые им в повседневной жизни не пользуются). Теперь же потребуется немного углубить знания, выучив её вплоть до 16 × 16.
И последнее: я убеждён, что рядовому пользователю эти навыки не понадобятся с вероятностью 99.…%. В общем, вы предупреждены  .
.

Таблица умножение от 11 до 16
| 11
11 × 2 = 22 11 × 3 = 33 11 × 4 = 44 11 × 5 = 55 11 × 6 = 66 11 × 7 = 77 11 × 8 = 88 11 × 9 = 99 11 × 10 = 110 11 × 11 = 121 11 × 12 = 132 11 × 13 = 143 11 × 14 = 154 11 × 15 = 165 11 × 16 = 176 |
12
12 × 2 = 24 12 × 3 = 36 12 × 4 = 48 12 × 5 = 60 12 × 6 = 72 12 × 7 = 84 12 × 8 = 96 12 × 9 = 108 12 × 10 = 120 12 × 11 = 132 12 × 12 = 144 12 × 13 = 156 12 × 14 = 168 12 × 15 = 180 12 × 16 = 192 |
13
13 × 2 = 26 13 × 3 = 39 13 × 4 = 52 13 × 5 = 65 13 × 6 = 78 13 × 7 = 91 13 × 8 = 104 13 × 9 = 117 13 × 10 = 130 13 × 11 = 143 13 × 12 = 156 13 × 13 = 169 13 × 14 = 182 13 × 15 = 195 13 × 16 = 208 |
| 14
14 × 2 = 28 14 × 3 = 42 14 × 4 = 56 14 × 5 = 70 14 × 6 = 84 14 × 7 = 98 14 × 8 = 112 14 × 9 = 126 14 × 10 = 140 14 × 11 = 154 14 × 12 = 168 14 × 13 = 182 14 × 14 = 196 14 × 15 = 210 14 × 16 = 224 |
15
15 × 2 = 30 15 × 3 = 45 15 × 4 = 60 15 × 5 = 75 15 × 6 = 90 15 × 7 = 105 15 × 8 = 120 15 × 9 = 135 15 × 10 = 150 15 × 11 = 165 15 × 12 = 180 15 × 13 = 195 15 × 14 = 210 15 × 15 = 225 15 × 16 = 240 |
16
16 × 2 = 32 16 × 3 = 48 16 × 4 = 64 16 × 5 = 80 16 × 6 = 96 16 × 7 = 112 16 × 8 = 128 16 × 9 = 144 16 × 10 = 160 16 × 11 = 176 16 × 12 = 192 16 × 13 = 208 16 × 14 = 224 16 × 15 = 240 16 × 16 = 256 |
Следующим шагом необходимо соотнести десятичные числа от 10 до 15 с шестнадцатеричными цифрами от A до F.
Таблица соответствия шестнадцатеричных цифр
| HEX (шестнадцатеричная) | DEC (десятичная) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| A | 10 |
| B | 11 |
| C | 12 |
| D | 13 |
| E | 14 |
| F | 15 |
А теперь вспомним поразрядное умножение из предыдущей статьи, для цифры 7. Здесь будет лишь поправка на другую систему счисления (не на 10, как там, а на 16).
Обычно в компьютерной литературе, для однозначного указания основания системы счисления, применяется следующая нотация:
— шестнадцатеричное число — 0x100 (256 в десятичной, признак — 0x в начале)
— десятичное число — 100 (наша, человеческая, система счисления)
— восьмеричное число — 0100 (64 в десятичной, признак — ведущий ноль)
— двоичное число — 0b100 (4 в десятичной, признак — 0b в начале)
Преобразование шестнадцатеричного числа в десятичное
Для начала, небольшой рисунок:
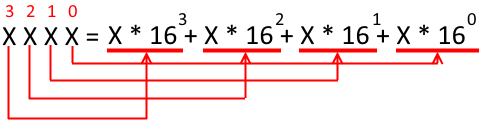
Для преобразования требуется каждую цифру числа умножить на «разряд», в котором оно находится. Из курса начальной школы мы помним, что позиции, занимаемые в числовой строке, называются (справа налево) единицы, десятки, сотни и т. д. Здесь почти то же самое, но с поправкой на систему счисления. Каждый следующий разряд — это +1 степень текущей системы счисления. Любое число в степени ноль — это ноль, в степени 1 — самом число, в степени 2 (квадрат) — число, умноженное само на себя и т. д.
Для наглядности привожу пример. Допустим, возьмём шестнадцатеричное число 0x1F8. Нам требуется перевести его в десятичную систему, поэтому запишем (0x — это признак основания!):
1F816 = 116 × 162 + F16 × 161 + 816 × 160 = 1 × 256 + 15 × 16 + 8 × 1 = 256 + 240 + 8 = 504
Обе таблички нам пригодились: благодаря второй мы переводим числа из шестнадцатеричной системы в десятичную, благодаря первой — легко перемножаем «больше» числа.
Небольшое отступление
А знаете ли вы, что у нас сейчас могла бы использоваться двенадцатеричная система счисления, используемая ещё шумерцами? По одной и версий, этому способствовало количество фаланг пальцев руки. Взгляните на рисунок:
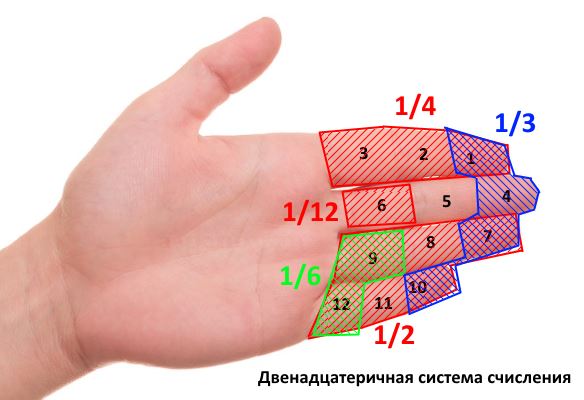
Скорее всего, вам сложно это представить. Но, взглянув на это под другим углом, можем убедиться, что выбор был бы очень хорош, ведь 12 делится без остатка на 2, 3, 4, 6 (в то время, как 10 можно разделить лишь на 2 и 5). Естественно, умножения и деления на степень числа 12 были так же просты, как сейчас аналогичные операции для степени числа 10.
Выучив эти таблицы, любой человек легко сможет переводить компьютерные байты в привычные числа. При желании, как следует потренировавшись и «расширив объём» краткосрочной памяти, станут доступны и более сложные варианты. Но, как уже говорилось чуть ранее, манипуляции с байтами мало кому нужны, не говоря о чём-то большем.

днём интернета

шоколадкой для работы мозга

коробочкой ароматного чая для бодрости

продлением хостинга на +1 месяц






Мне всегда было интересно, почему 12-ричная система удобна. Ведь поэтому она и существует? Теперь немного стало понятнее. Хотя мне конечно все эти переводы ни к чему. Однако прочитала с удовольствием, очень познавательно!
Надежда, именно с точки зрения практического применения. А то какое «удобное» число не берёшь , ни на 3 нацело не поделишь, ни на 4, ни на 6.
Но сейчас маловероятно, что наша система изменится. Слишком многое уже на неё завязано. Скорее уж бриты на километры перейдут.
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.
Здравствуйте.
Вы правы. Таким способом можно переводить не только из шестнадцатеричной системы, но и любой другой. В примерах у меня именно так и есть.